Uncertain Volatility Derivative Model Based on the Polynomial Chaos
Στο επιστημονικό περιοδικό «Journal of Mathematical Finance», παρουσιάζεται, η μέθοδος που ανέπτυξα, σύμφωνα με την οποία η μεταβλητότητα λαμβάνεται υπόψιν ως πεδίο τυχαιότητας στον υπολογισμό των χρηματοοικονομικών παραγώγων.
Ειδικότερα, το 1973 οι Robert Merton και Myron Schole, σε στενή συνεργασία με τον Fischer Black, ανέπτυξαν τη μέθοδο αποτίμησης δικαιωμάτων προαίρεσης και τον προσδιορισμό της αξίας των παραγώγων, η οποία και τους οδήγησε στην κατάκτηση του Νόμπελ Οικονομίας το 1997. Παρά την κριτική που έχει δεχθεί, η μέθοδος αυτή, παραμένει έως και σήμερα, το βασικό εργαλείο των αγορών για την εκτίμηση της αναδιανομής του ρίσκου, όσων είναι πρόθυμοι να το αναλάβουν.
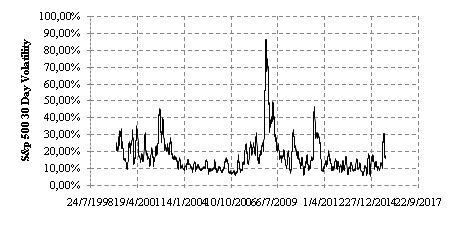
Βασικό μειονέκτημα της μεθόδου, είναι ότι χρησιμοποιεί τη μεταβλητότητα των προϊόντων ως σταθερή παράμετρο, γεγονός που δεν είναι δυνατό να συμβεί στην πράξη, ειδικά σε περιόδους κρίσεων και έντονης αβεβαιότητας.
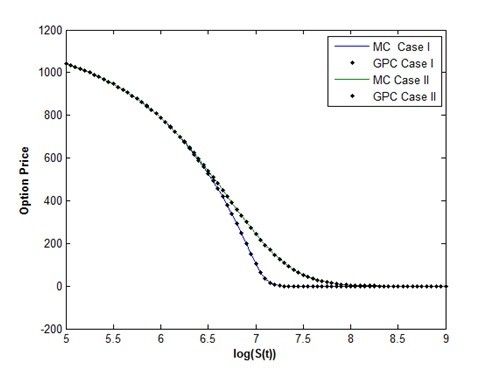
Στο επιστημονικό περιοδικό «Journal of Mathematical Finance», παρουσιάζεται η μέθοδος που ανέπτυξα, σύμφωνα με την οποία η μεταβλητότητα λαμβάνεται υπόψιν ως πεδίο τυχαιότητας. Κάνοντας χρήση των γενικευμένων πολυωνύμων του χάους, είναι εφικτή, η εκτίμηση της τιμής του παραγώγου, ακόμη και σε περιόδους που χαρακτηρίζονται από έντονη αβεβαιότητα!
Διαβάστε περισσότερα: Uncertain Volatility Derivative Model Based on the Polynomial Chaos